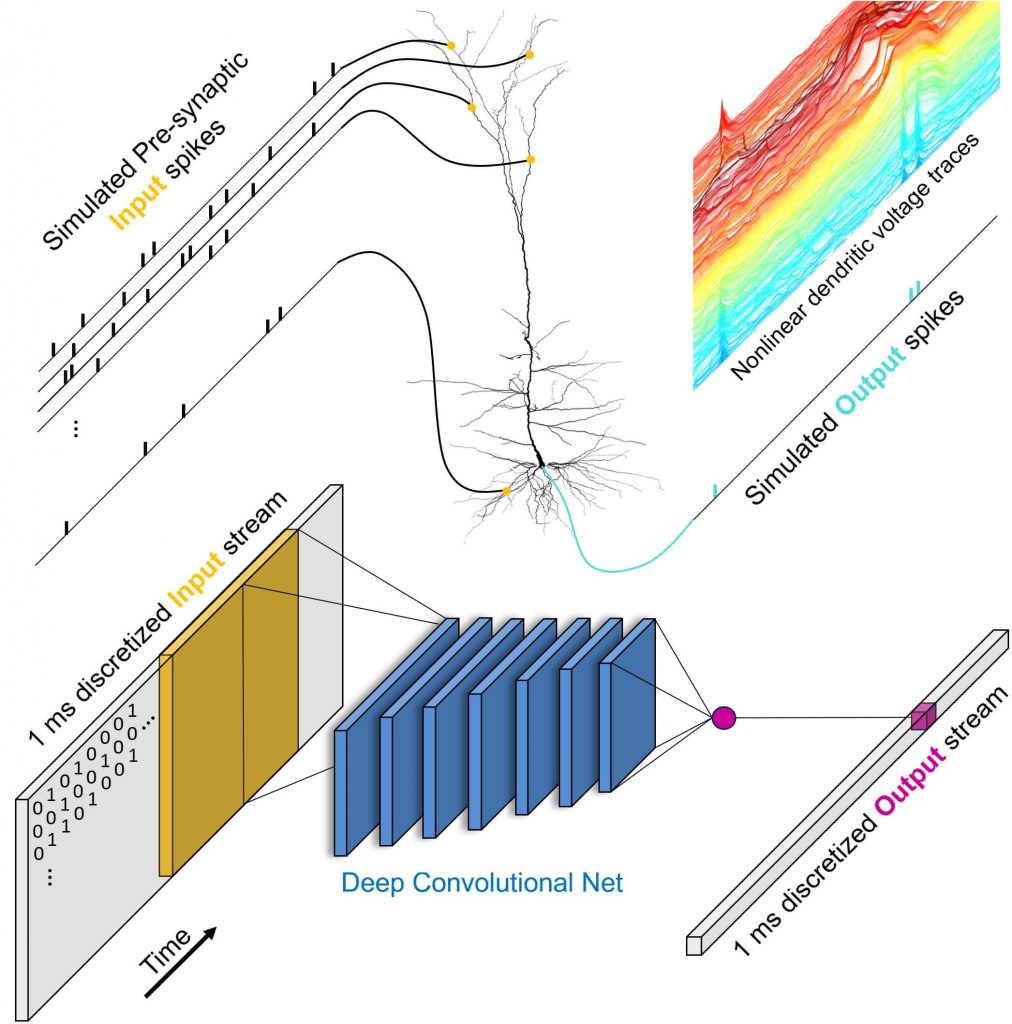
Neurons are building blocks of brains. But neurons are themselves complex, spatially-distributed machines. Using recent advances in machine learning, we introduce a systematic approach to characterize the function of such complex neurons. Our approach uses deep neural networks (DNNs) to recapitulate the way by which neurons transform their inputs to spikes. The resulting DNN provides a substantially more transparent view of the function of the neuron, and in this way generates deep insights into the neuronal integration mechanisms. To accomplish these goals, we used detailed models of cortical neurons to generate large training sets of inputs and of the corresponding outputs of the neurons at millisecond resolution, the temporal resolution of the biological output of neurons (spikes). We then trained DNNs to faithfully reproduce the training data. In one example, we used a realistic model of a layer 5 cortical pyramidal cell (L5PC) for this purpose. These neurons are among the largest and most complex in the neocortex. The DNN that was trained to mimic this neuron generalized well when presented with inputs that differed substantially from those in the training set, showing that the DNN indeed captured fully the complexity of the neuron. The resulting DNN was rather complex: a temporally convolutional DNN with five to eight layers was required. However, when one specific component of the synapses on these neurons, the NMDA receptors, were removed from the L5PC model and the DNN retrained, a much simpler network (fully connected neural network with one hidden layer) was sufficient to fit the neuron. Thus, NMDA receptors play an important role in shaping the complexity of the integration mechanisms of neurons in cortex. We also analyzed the principles of input integration on dendritic branches, showing that it could be conceptualized as pattern matching from a set of spatiotemporal templates. This study provides a unified characterization of the computational complexity of single neurons and suggests that the architecture of cortical networks is specialized for supporting their spectacular computational power.