Place cells in the hippocampus are neurons that represent the position of an animal as it forages in space. It is hypothesized that the place cells’ synaptic connections are set up such that the system can maintain an ongoing memory of the animal’s position: Each pattern of neural activity that corresponds to a particular position (in any one of the environments with which the animal has become familiar) can be sustained in persistent neural activity, even if the external sensory cues are removed. One interesting aspect of this place cell representation is that completely different patterns of activity are used to represent positions in distinct environments: for example, two place cells may be active in nearby locations for one environment, but for another environment they may be active in distant locations.
Neural network models for the hippocampal network have existed for several decades, yet these models are not able to sustain the persistent states that correspond to all possible positions in multiple environments; attempting to embed all of these memories causes undesirable interference. This means that the activity patterns that correspond to most locations are not truly persistent; instead, they slowly drift to represent other nearby locations, thereby degrading the memory of the position. The present work shows that by tweaking the synaptic connectivity between neurons, it is possible to greatly improve the stability of the memory representations. The outcome is a nearly continuous set of steady activity patterns, which corresponds to all possible positions in a large number of environments.

Figure 1: Theoretically, it is known how to construct a neural network that has a continuum of stationary activity patterns, each corresponding to a unique position in space. These states can be conceptualized as the minima of an abstract “energy function”, here illustrated as a one-dimensional valley in the space of all possible neural activity patterns (Figure 1a). Due to the embedding of multiple such representations in the network (each corresponding to a different environment), the valley becomes “wrinkled” (Figure 1b), and only a few patterns of activity are stable, corresponding to the minima of the wrinkled trough on the right.

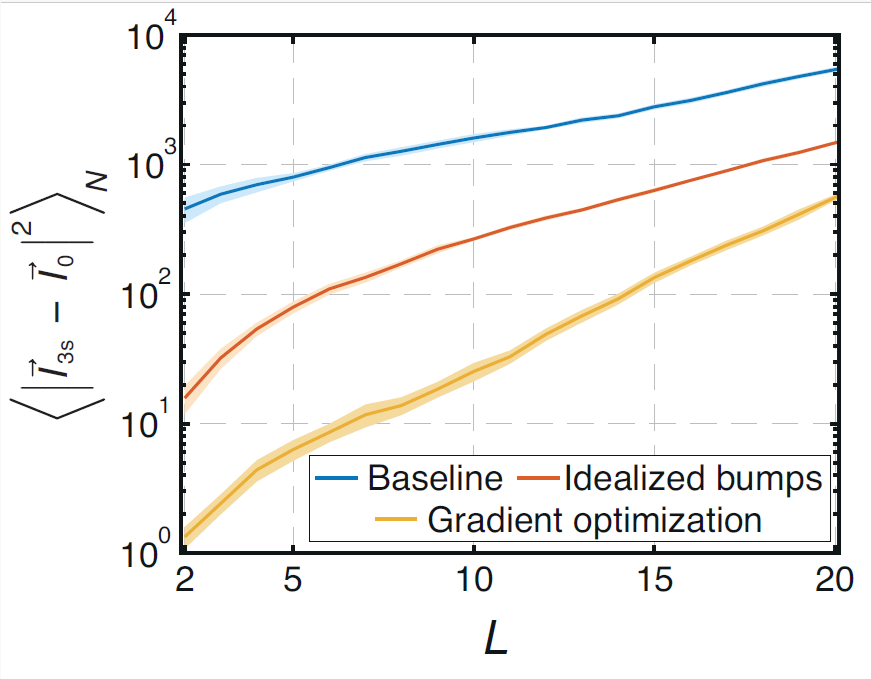
Figure 2: Quantification of the stability of all memory representations in a standard model of hippocampal activity as a function of L, the number of embedded environments (blue trace). The red and yellow traces correspond to the “Idealized bumps” method and the “Gradient optimization” method, respectively, which are two methods for tweaking the connectivity. As we discuss in the paper, these tweaks lead to dramatically improved stability. Small values correspond to high stability, and the vertical axis is logarithmic.