In this paper, we pursue the hypothesis that geometric properties of neuronal representations are natural-order parameters for understanding the neuronal processing of high cognitive functions, and for comparing learning and computations in brains and artificial neural networks. In the first part of this paper, we discuss the geometric properties of neural manifolds that are necessary and sufficient for good generalization capabilities in the context of object recognition tasks. In the second part of the paper, we review recent advances in the theory of learning in fully connected deep wide networks, and compare the predictions of these theories regarding the geometry of learned representations against our results on object neural manifolds, and conclude by suggesting future directions of analyzing feature learning in more complex DNNs.
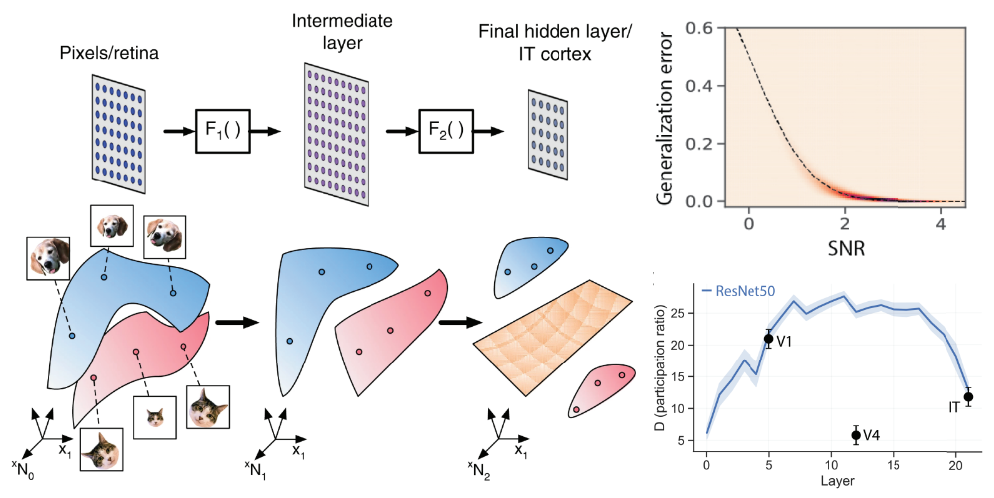
Figure 1: Topological and geometrical properties of neural population responses (known as neural manifolds) change across the neural hierarchy, thus transforming object manifolds that are not linearly separable (in the first and intermediate layers) into separable object manifolds (in the last layer) Changes in neural manifolds across the hierarchy can be quantified by several geometric metrics. In the case of “few-shot” learning, the geometric metrics of the manifolds determine the signal-to-noise ratio (SNR), which predicts the generalization performance. One important geometric metric, the dimension (D) of the manifold, expands dramatically in early layers and contracts in later layers the dimensionality first contracts from V1-like layer to V4, then expands from V4 to IT.
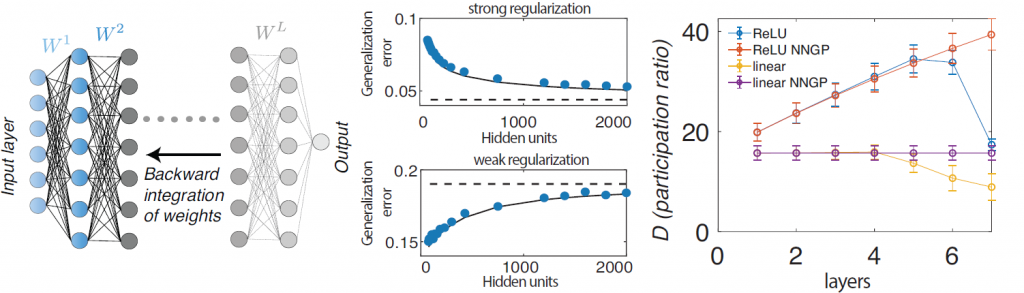
Figure 2: The theory of learning in deep neural networks reveals how learning changes the generalization performance and shapes the hidden representation. In the back-propagating kernel renormalization (BPKR) approach, the generalization error of the network is calculated by averaging across the distribution of the network weights after learning, and a renormalization factor is introduced at each step during backward integration until all the network weights are averaged out. This approach yields an accurate theoretical prediction of the generalization error in networks with different widths and that were trained with different regularization strengths. The theory also captures the changes in the hidden representation and the geometric metrics of the neural manifolds. In fully connected networks with ReLU nonlinearity, the theory predicts that the dimensionality of the neural manifolds first expands in early layers and contracts in the later layers, similar to what has been found in a pretrained ResNet50.


